Probabilidade Part-1

Determinístico

A sequência recursiva, amplamente utilizada em campos como matemática e ciência da computação, destaca-se pela previsibilidade de seus elementos, devido sua regra de construção. A capacidade de antecipar com precisão qualquer elemento torna essa abordagem valiosa em modelagem de padrões e processos iterativos.

Quanto a modelos determinísticos, podemos destacar a possibilidade de repetições, onde conhecendo-se a semente inicial e a regra de construção podemos predizer o seu comportamento. Esse conceito, presente em fundamentos físicos como eletricidade, mecânica e cinemática, permite a previsão exata da saída de experimentos sob condições iniciais conhecidas.

Probabilístico

A transição para experimentos aleatórios introduz a incerteza, onde a predição exata da saída torna-se impossível. No entanto, os modelos probabilísticos entram em cena, permitindo a determinação das probabilidades associadas a cada possível resultado. Mesmo diante da imprevisibilidade individual de cada experimento, a análise de um grande conjunto de dados revela padrões.

Conceitos fundamentais, como espaço amostral e eventos, fazem parte do cenário probabilístico. O espaço amostral é o conjunto de saídas possíveis, enquanto eventos representam os elementos desse conjunto. A relação entre eventos é definida por situações como evento impossível, evento certo, união e interseção, e a complementaridade (não ocorrer) de um evento.

Exemplo

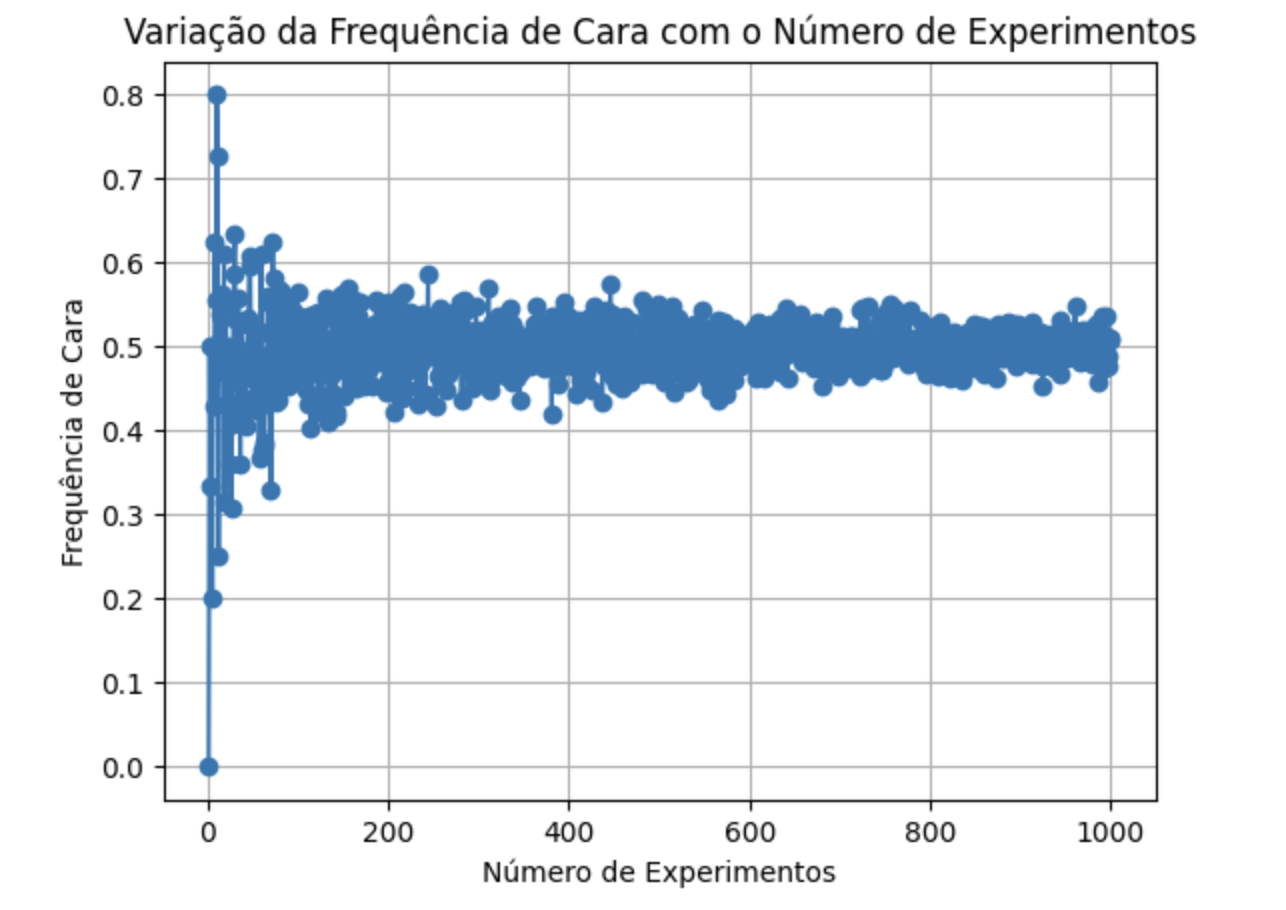
Qual a frequência com que sai cara frente ao número de experimentos?

import numpy as np
import matplotlib.pyplot as plt

def coin_toss():
    result = np.random.choice([{1: 'cara'}, {0: 'coroa'}])
    return result

def is_heads(coin_toss_result):
    return coin_toss_result.get(1) == 'cara'

def experiment(n_attempts):
    arr_results = []

    for _ in range(n_attempts):
        coin_toss_result = coin_toss()
        arr_results.append(coin_toss_result)
    return arr_results

def n_heads(experiment_result):
    result = 0
    for coin_toss_result in experiment_result:
        if is_heads(coin_toss_result):
            result += 1
    return result

# Número máximo de experimentos
max_attempts = 1000

# Listas para armazenar os resultados
num_experiments = []
head_frequencies = []

# Realizar os experimentos variando o número de tentativas
for n_attempts in range(1, max_attempts + 1):
    results = experiment(n_attempts)
    head_count = n_heads(results)
    
    # Calcular a frequência de caras
    head_frequency = head_count / n_attempts
    
    # Armazenar os resultados
    num_experiments.append(n_attempts)
    head_frequencies.append(head_frequency)

# Criar o gráfico de linha
plt.plot(num_experiments, head_frequencies, marker='o')
plt.xlabel('Número de Experimentos')
plt.ylabel('Frequência de Cara')
plt.title('Variação da Frequência de Cara com o Número de Experimentos')
plt.grid(True)
plt.show()

Plot