Probabilidade Part-2 (Teorema Bayes)

Distribuição Condicional

Se já sabemos que um evento X ocorreu, isso pode (ou não) mudar a probabilidade de outro evento Y. Definindo a nova probabilidade como P(Y|X)(probabilidade de Y dado X)

Problema Proposto

Imagina que temos um teste que detecta se temos ou não câncer. Esse teste tem uma acurácia de 90% para qualquer um dos lados. O que isso significa:

• Se a pessoa tem câncer e faz o teste, 90% dos casos o teste diz que a pessoa tem câncer.
• Se a pessoa não tem câncer e faz o teste, 90% dos casos o teste diz que a pessoa não tem câncer.

Vamos a questão:

Uma pessoa fez o teste e foi diagnosticada com câncer. Qual a probabilidade dessa pessoa ter câncer? (Em um primeiro momento a maioria das pessoas cai em uma armadilha instintiva, responendendo que a probabilidade é de 90%.)

Porque do erro:

O problema é que falta uma informação para responder a questão, que é:

• Qual a porcentagem da população que tem câncer?

Vamos aplicar em um cenário hipotético

• Vamos imaginar que 1% da população tem câncer;
• Vamos imaginar que temos uma população de 1000 pessoas;

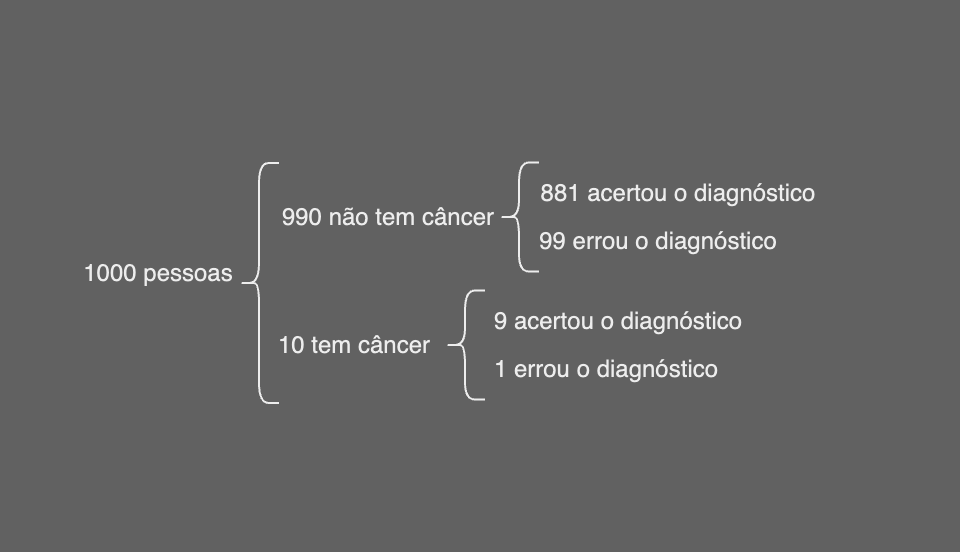
Nesse cenário a quantidade de pessoas que o teste diagnosticou com câncer foi de: 108 pessoas. Mas dessas 108 pessoas apenas 9 de fato tem câncer. Então qual a probabilidade da pessoa ter câncer, nesse nosso cenârio?

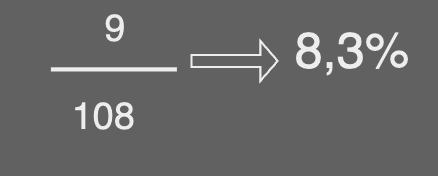
O motivo dessa porcentagem está no fato de que apenas 1% da população tem câncer. Mesmo o teste ter uma acurácia alta ele gerou um grande número de falsos positivos, sendo maior que a quantidade de pessoas que o teste diz ter a doença.

Teorema de Bayes

O teorema de Bayes é o método principal para compreender a probabilidade de algum evento, P(A|B), dado alguma nova informação, P(B|A), e uma crença prévia na probabilidade do evento, P(A):

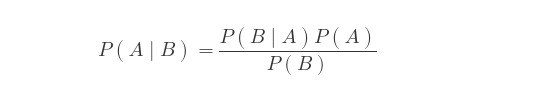
Vamos aplicar o teorema no nosso problema

Nossos eventos:

• A Probabilidade de ter câncer;
• B Probabilidade do teste dar positivo;